- 太友SPC系統
(QSmart? SPC Monitor) - 太友質量管理系統
(QMS系統-QCData?) - 關于太友
- 聯系我們
- 全國總機:400-100-8648
廣州熱線:020-85530201
(Confounding the 2k Factorial Design in Four Blocks)
建構一個交絡于4個集區而每個集區有2k-2個觀測值的2k因子設計是有可能的,這種設計對于因子個數k>= 4而集區大小卻相當小時特別有效。
茲考慮25設計,如每個集區只能容納8次試驗,則需要4個集區,選出2個效果交絡于集區,如ADE與BCE,此二個效果所對應之定義對比為,
L1 = x1+ x4 + x5
L2 = x2+ x3 + x5
則每一個處理組合會產生一個L1 (Mod 2)與L2 (Mod 2)的特定成對值,即(L1 , L2)= (0, 0), (0, 1), (1, 0),或(1, 1),產生相同的(L1 , L2)值的處理組合將被指訂至同一集區,如,
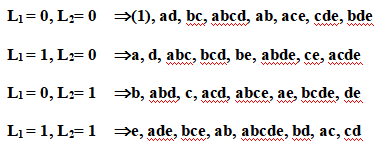
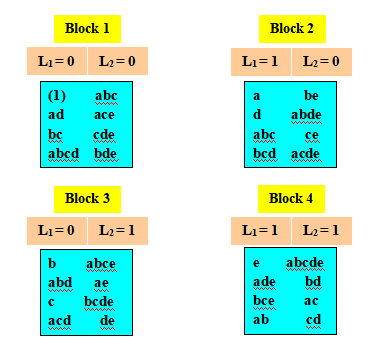
圖7-5 交絡ADE, BCE與ABCD之4個集區之25設計
仔細思量,除了ADE與BCE外,尚有另一個效果被集區交絡,因4個集區有3個自由度,而ADE與BCE各有1個自由度,明顯地另有一個1個自由度的效果亦被交絡矣,此即ADE與BCE的廣義交互作用(Generalized Interaction),其定義為ADE與BCE的乘積Mod 2,因此,ADE與BCE的廣義交互作用為(ADE)(BCE) = ABCDE2 = ABCD ,且亦交絡于集區。
注意,對某個特定集區里的任何2個效果的符號相乘(e.g., ADE與BCE)帶來該集區另一個效果的符號(即ABCD)。因此,ADE,BCE與ABCD都是交絡于集區。
由25設計的正負符號,可知處理組合被指派至集區如下
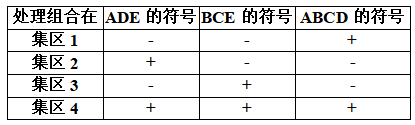
在上節7-4中提及之主集區的群理論性質仍成立,主集區里的2個處理組合的乘積產生主集區里的另一個元素,亦即,如,
ad × bc = abcd; abe × bde = ab2de2 = ad
要建構另一集區,則選一個不在主集區里之處理組合(如b)與主集區里的處理組合乘以b,則,
b × (1) = b; b × ad = abd;
b × bc = c; b × abcd = acd
如此會產生集區3里之8個處理組合。實務上,主集區可以從定義對比與群理論性質得到,而其他集區之處理組合由
述方法決定。建構一個4集區的2k設計的一般步驟:
◎ 選擇2效果與集區交絡,自然會有第3個效果(即是前2個的廣義交互作用)與集區交絡,
◎ 利用2個定義對比(L1 , L2)與主集區的群理論性質來建構所要的設計,
◎ 在選擇交絡于集區之效果時務必謹慎,以免有興趣的效果被交絡。
犧牲3因子交互作用的信息比犧牲2因子交互作用更合意
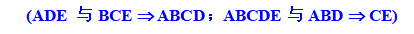
2021/1/14 16:29:57
2021/1/27 17:05:39
2021/3/10 15:48:49
2021/4/8 14:42:32
2021/1/8 16:32:33

我們不單提供專業的軟件與服務,我們同時也為客戶系統的運行提供理論與經驗支持,分享我們在質量管理領域的相關經驗與知識!