手机看黄av免费网址-亚洲国产美女精品久久久久∴-日本丰满大乳乳液-夜夜揉揉日日人人

當因子數目很小時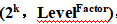，如k = 2或3，通常有必要反覆實驗以獲得一個誤差估計值。如23因子實驗必須以2個集區來進行且ABC被交絡，實驗者決定反覆設計4次，如下圖，

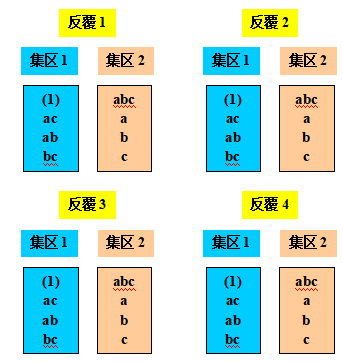
此設計總共32個觀測值和31個自由度，有8個集區即7個自由度，此7個自由度分解為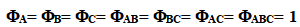，而誤差平方為反覆與因子效果(A, B, C, AB, AC, BC)之二者交互作用。

考慮視交互作用為零且將其均方作為誤差估計值的作法是成立的，此均方誤差可以檢定主效果與2-因子交互作用效果。

倘實驗資源允許反覆的交絡設計，較佳方式是稍微以不同方式來設計各個反覆的集區，此方式包括在每個反覆中交絡不同的效果，使得所有的效果都能有一些信息，此法稱之為部分交絡(Partial Confounding)。倘k 不算太小，即k 3 4，且只一次反覆時，實驗者常假設高階交互作用效果是可忽略的，并將其平和合并為誤差。

范例7-2

回顧再續范例6-2，一個化學產品于一壓力槽內生產，在實驗工廠進行因子實驗來研究產品的過濾比率(Filtration Rate)，4個因子為溫度(A)、壓力(B)、甲醛濃度(C)、與攪拌速度(D)，各因子均有2水平，單次反覆。有興趣于極大化過濾比率。

用此實驗來說明一個未反覆設計集區劃分與交絡的概念，假設2⁴ = 16種處理組合無法利用一批原料進行所有的試驗，實驗者由一批原料可以試驗8個處理組合，所以一個2⁴ 交絡于2個集區的設計是適當的，且交絡最高階交互作用效果(ABCD)于集區。

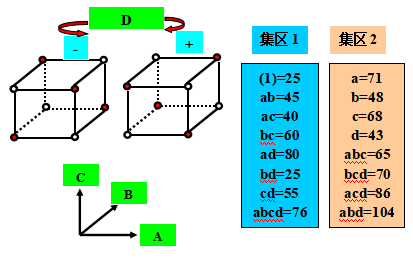
假設二批原料中有一批的質量低劣，造成所有的反應值均比用另一批原料所得值低20，即原始反應值減去20，低劣質量原料是集區1與良好質量原料批為集區2。計算結果，

◎ 4個主效果、6個2-因子交互作用效果、4個3-因子交互作用效果的估計值均與無集區效果的例6-2所得之效果估計值完全相同。當劃出這些效果估計值的常態機率圖時，因子A、C、D與AC、AD交互作用為顯著重要效果。

◎ ABCD交互作用效果的估計值原為1.375，但在此實驗其估計值為-18.625，因ABCD交絡于集區，ABCD交互作用效果的估計值是原1.375加上區集效果(-20)，即ABCD = 1.375+(-20)= -18.625。集區效果亦可由二個集區平均反應差得之，即

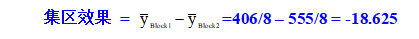
所以，此效果真正估計= 集區 + ABCD

◎ 此實驗倘非以集區方式進行，且前8次試驗均減去20，則結果可能會非常不同。