手机看黄av免费网址-亚洲国产美女精品久久久久∴-日本丰满大乳乳液-夜夜揉揉日日人人

簡介 (Introduction)

有多種情況實驗者無法在均一的條件下進行2k因子實驗的所有試驗，如原料不足、或故意改變實驗條件，以確保處理于實際上可能遇到的狀況能一樣地有效(i.e., 即穩健的)。此種情況用到的設計技巧是集區劃分(Blocking)，本章集中于2k因子設計的一些特殊的集區劃分技巧。

集區劃分一個反覆的2k因子設計

(Blocking a Replicated 2k Factorial Design)

假設2k因子設計反覆n次，此情況與第5章討論的完全相同，每一種不同的條件就是一個集區，而每個反覆就在集區內，在各個集區(或反覆)的試驗以隨機順序進行。

范例 7-1

考慮在6-2節所描述一反應濃度(Reaction Concentration)和觸媒量(Catalyst)對化學反應過(制)程合格率效果的研究。假設單一批原料只容納4次試驗，所以，需要3批原料來進行3次反覆，其中每一原料批對應到一個集區， 

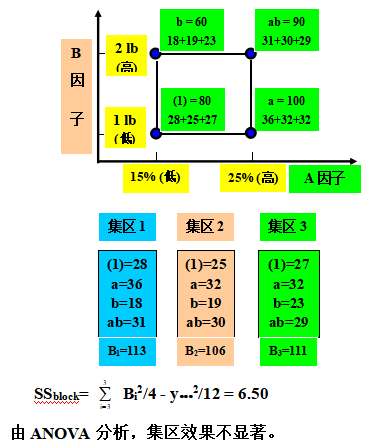
2k因子設計的交絡(Confounding in the 2k Factorial Design)

許多情況是在一個集區里進行一次完整的2k因子設計是不可能的。交絡(Confounding)是一個設計技巧，可安排一個完整的因子實驗到數個集區，其中集區的大小是小于一次反覆中處理組合的個數，此技巧造成某些處理效果(通常指高階交互作用)的信息成為無法區分于(In-distinguishable from)或交絡于(Confounded with)集區效果。本章集中于2k因子設計的交絡系統。

2k因子設計交絡于2個集區

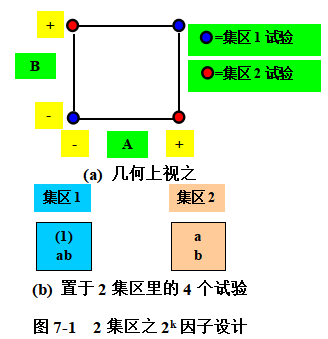
上圖(a)顯示相對對角的處理組合被安置到不同的集區，圖(b)視出集區1包含處理組合(1)與ab、集區2包含處理組合a與b，當然，在集區里處理組合的試驗順序是隨機決定的，且隨機決定集區順序。則A與B的主效果(與似無發生集區般)為，

A = [ab+a-b-(1)]/2

B = [ab+b-a-(1)]/2

A與B均無受到集區劃分的影響，因為上式中各有來自每個集區的一個正的與一個負的處理組合，亦即，集區1與集區2之間的任何差異均被抵消矣。

續考慮AB交互作用效果

AB = [ab+(1)-a-b]/2

因2個正號的處理組合[ab與(1)]在集區1里、而2個負號的處理組合[a與b]在集區2里，集區效果與AB交互作用效果是完全相等的，亦即，AB是交絡于集區。

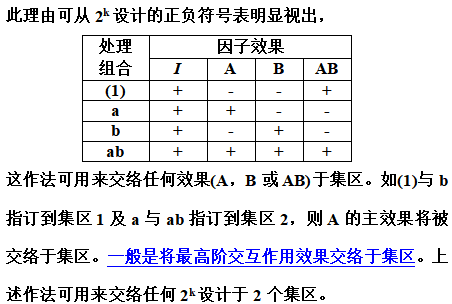
建構集區的其他方法

(Other Methods for Constructing the Blocks)

此為利用線性組合，

L = a1x1+ a2x2 + …+ akxk    (7-1)

其中xi是出現在處理組合中第i個因子的水平，與ai是要被交絡的效果中第i個因子的冪次(Exponent)。對2k系統，ai = 0或1，及xi= 0 (低水平)或xi= 1 (高水平)。式(7-1)稱之為定義對比(Defining Contrast)，會產生相同L(Mod 2)的可能值只有0與1，如此指訂2k個處理組合正好到2個集區里。

茲考慮23設計而且交絡ABC于集區，在此x1對應A、x2對應B、x3對應C，與a1 = a2 = a3 =1，因此，對應于ABC的定義對比為，

L = x1+ x2 + x3 

因此處理組合(1)在(0,1)的符號表示下為000；所以，

L = 1(0)+1(0)+1(0)= 0 = 0   (Mod 2)

同理，處理組合a為100；所以，

L = 1(1)+1(0)+1(0)= 1 = 1   (Mod 2)

故(1)與a將分屬不同的集區。對于其他的處理組合，

b:  L = 1(0)+1(1)+1(0)= 1= 1   (Mod 2)

ab:  L = 1(1)+1(1)+1(0)= 2 = 0   (Mod 2)

c:   L = 1(0)+1(0)+1(1)= 1= 1   (Mod 2)

ac:  L = 1(1)+1(0)+1(1)= 2 = 0   (Mod 2)

bc:  L = 1(0)+1(1)+1(1)= 2 = 0   (Mod 2)

abc:  L = 1(1)+1(1)+1(1)= 3 = 1   (Mod 2)

所以，(1), ab, ac, bc屬于集區1；a, b, c, abc屬于集區2，這與用正負符號表所產生的設計完全相同。

另一種建構這些設計的方法，包含處理組合(1)的集區稱之為主集區(Principal Block)，在此集區里的處理組合有一個很有用的群理論性質(Group-Theoretic Property)，即它們以乘法Mod 2的運算而形成之一”群”(Group)，此意謂著主集區內的任何元素[除(1)外]可由主集區內任2個元素(處理組合)